La función de respuesta de frecuencia
Es una cantidad
tridimensional que consiste en amplitud vs fase vs frecuencia. Por eso una
gráfica verdadera de ella necesita tres dimensiones, lo que es difícil de
representar en papel. Una manera de realizar esto es la llamada gráfica de
Bode, que consiste en dos curvas, una de amplitud vs frecuencia, y una de fase
vs frecuencia. Otra manera de ver la función es de resolver la porción de fase
en dos componentes ortogonales, una parte en fase (llamada la parte real) y una
parte 90 grados fuera de fase (llamada la parte imaginaria o parte de la
cuadratura).
A continuación vamos a ver una forma muy común de representar las funciones de transferencias: los diagramas de Bode. Veremos su definición, el por qué de su uso, y sus posibles aplicaciones.
Diagramas de Bode
Ya hemos visto las representaciones gráficas del módulo y del argumento en función de la pulsación. Otro tipo de gráficas que son muy útiles son los diagramas de Bode en los que se usan escalas logarítmicas en y en ω. Estos diagramas tienen la misma información, pero son más sencillos de escribir, ya que se pueden aproximar mediante líneas rectas.
Si tenemos la magnitud:
Tomaremos logaritmos neperianos con el fin de acabar con los exponentes de forma que tendremos:

Aqui se convertido en una suma de una parte real (dependiente sólo del módulo y una imaginaria (función sólo de la fase).
La transformación de ln a log es: dB = 8,6859 x neperios
Aplicación
Si tenemos la función de transferencia
si tomamos ln:
a) si ω << z:
b) si ω >> z: Tendremos una recta de pendiente 20 dB/década y se corta con la recta de 0 dB cuando

Las frecuencias entre el punto B y el punto A abarcan una década. La desviación máxima entre la aproximación y la real es de 3dB.
En cuanto a la parte imaginaria de  :
:
Se representa como dos rectas: una a 0º para ω << z y otra a 90º para ω >> z, unidas por una recta de pendiente 45º/década, que pasa por el punto (log z, 45º)
Debido a las escalas empleadas en los diagramas de Bode, éstos pueden ser construidos en forma aproximada mediante trazos rectos. La figura C.1 muestra los diagramas de Bode aproximados para funciones sencillas de orden 1.
La figura C.2 muestra los diagramas de bode para funciones de orden 2; en estos casos, las aproximaciones pueden ser bastante lejanas de los diagramas exactos, dependiendo del factor de amortiguamiento  . Por esta razón se han trazado los diagramas exactos para una función de segundo orden (para el primer caso de la figura C.2), en las figuras C.3 y C.4
. Por esta razón se han trazado los diagramas exactos para una función de segundo orden (para el primer caso de la figura C.2), en las figuras C.3 y C.4
Para funciones de transferencia más sofisticadas que las de las figuras C.1 y C.2 se descompone la función de trasferencia como productos de términos más sencillas, se trazan los diagramas de bode estas de funciones y luego se suman punto a punto para obtener los diagramas de la función original
Ejemplo Considérese la función de transferencia
Esta función puede descomponerse como el producto de cuatro funciones de transfenecia más sencillas:
Cada una de las funciones , , y son de la forma que se muestra en las figuras C.1 y C.2. Pueden trazarse los diagramas de bode aproximados de estas funciones, y luego sumarlos punto a punto para obtener los diagramas de 
Ejemplos de funciones de
transferencia


La representación de H(ω) implica 2 gráficas (módulo |H(ω)| y fase ((ω)). Son magnitudes reales → tienen significado físico.
Forma de H(ω): Cociente de dos polinomios en ω (jω)
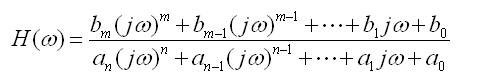
Factorizando los polinomios:
Representaremos el módulo y la fase de
H(ω) factorizada
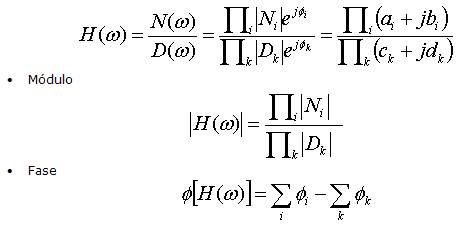
Por comodidad, se escoge una representación logarítmica:
Módulo:
eje Y: A(dB)=20log(|H(ω|) (decibelios)
eje X: ω en escala logarítmica
Fase:
eje Y: [H(ω)] en escala lineal
eje X: ω en escala logarítmica
(gráfica semilogarítmica)
Cada una de estas representaciones gráficas representa el Diagrama de Bode de Módulo y de Fase, respectivamente.
Aplicando logaritmos podemos representar el módulo de H(ω) como suma y diferencia de factores
Utilidad de los diagramas de Bode
Representación gráfica del comportamiento en frecuencia de
un circuito.
Permiten representar un rango de ω mucho mayor. Cuando los
polos y ceros de H(ω) son reales (o están muy cerca del eje R), la gráfica de
|H(ω)| y ([(ω)] se puede aproximar fácilmente por tramos lineales.
Análisis de Estabilidad utilizando
el Diagrama de Bode
Vídeo Explicativo
Estabilidad según Bode
Las trazas de Bode de una función de transferencia son una
herramienta gráfica de suma utilidad para el análisis y diseño de sistemas de
control lineales.
Ventajas:
En ausencia de un ordenador, las trazas de Bode se
pueden bosquejar por la aproximación de magnitud y fase con segmentos de línea
recta. 2. El cruce de ganancia, el cruce de fase, el margen de ganancia y el
margen de fase se determinan más fácilmente en las trazas de Bode que en la
traza de Nyquist. 3. Para propósitos de diseño, los efectos de añadir
controladores y sus parámetros se visualizan con mayor facilidad sobre las
trazas de Bode que sobre la traza de Nyquist.
Desventaja
La estabilidad absoluta y relativa a sistemas de fase
mínima se puede determinar desde las trazas de Bode, pero no así los de fase no
mínima. Por ejemplo, no hay forma de decir que el ángulo de 11 para el criterio de
Nyquist esté sobre las trazas de Bode.

No hay comentarios:
Publicar un comentario